Творчеству надо учить
Показаны сообщения с ярлыком Математика. Показать все сообщения
Показаны сообщения с ярлыком Математика. Показать все сообщения
среда, 5 августа 2015 г.
вторник, 4 августа 2015 г.
воскресенье, 2 августа 2015 г.
суббота, 1 августа 2015 г.
Математика Повторение Решаем уравнение, используя основное свойство пропорции
https://vk.com/math555 - видеоуроки по математике
https://vk.com/diststudent - группа дистанционного обучения
http://discriminant.jimdo.com - видеосправочник по математике и дистанционное обучение
Математика. Повторение. Решаем уравнение
Повторение - мать учения! Repetitio est mater studiorum!
Повторяем математику!
вторник, 29 июля 2014 г.
Наглядное пособие "Единицы массы"
Наглядное пособие "Единицы длины"
суббота, 22 марта 2014 г.
Текстовые задачи на среднюю скорость
При решении задач на среднюю скорость важно знать:
Средняя скорость — есть отношение всего пройденного пути ко всему затраченному времени.
ср
Рассмотрим примеры.
Средняя скорость — есть отношение всего пройденного пути ко всему затраченному времени.
- Если половину всего времени объект двигался со скоростью
, а вторую половину времени со скоростью 
, то средняя скорость ср находится как среднее арифметическое
ср- Если половину всего пути объект двигался со скоростью , а вторую половину пути со скорость , то находить среднее арифметическое скоростей нельзя!
Действительно, если обозначить весь путь за S, то
ср
Рассмотрим примеры.
Задачи на работу
Задачи на работу решаются с помощью одной-единственной формулы:
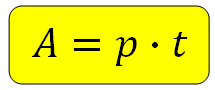
РАБОТА = ПРОИЗВОДИТЕЛЬНОСТЬ х ВРЕМЯ
Здесь
A — работа, t — время, а величина p, которая по смыслу является
скоростью работы, носит специальное название — производительность. Она
показывает, сколько работы сделано в единицу времени. Например, Вася
красит забор. Количество метров, которые он красит за час — это и есть
его производительность.
понедельник, 16 сентября 2013 г.
среда, 28 августа 2013 г.
Задачи на движение
Задачи на движение по водоёму.
Ученик с 5 класса должен знать:
Скорость по течению равна сумме собственной скорости и скорости течения реки.
Скорость против течения равна разности собственной скорости и скорости течения реки.
Скорость по озеру равна собственной скорости.
Собственная скорость равна половине суммы скорости по течению и скорости против течения.
Задачи на движение
Решение задач на движение двух тел в одном направлении.
Задача 1. Одновременно из одного пункта в одном направлении вышли два пешехода. Первый пешеход идёт со скоростью 6 км/ч, а другой – со скоростью 4 км/ч. Какое расстояние будет между пешеходами через 5 часов?
Решение: ? км
4 км/ч 5 ч. 6 км/ч
Скорость
|
Время
|
Расстояние
| |
1 пешеход
|
6 км/ч
|
5 ч
|
? км
|
2 пешеход
|
4 км/ч
|
5 ч
|
? км
|
1) 6*5=30 (км) – прошёл первый пешеход
2) 4*5=20 (км) – прошёл второй пешеход
3) 30-20=10 (км) - расстояние между пешеходами через 5 часов.
Ответ: 10 км.
Задачи на движение
Решение задач на встречное движение двух тел.
Задача 1. Одновременно из двух пунктов навстречу друг другу вышли два пешехода. Через 3 часа они встретились. Какое расстояние до встречи прошёл каждый пешеход и какое расстояние было между пунктами, если один пешеход шёл со скоростью 6 км/ч, а другой – со скоростью 4 км/ч?
? км
4 км/ч 6 км/ч
3 ч 3ч
Решение
Скорость
|
Время
|
Расстояние
| |
1 пешеход
|
4 км/ч
|
3 ч
|
?
|
2 пешеход
|
6 км/ч
|
3 ч
|
?
|
1)4*3=12 (км) – прошёл 1 пешеход
2)6*3=8 (км) – прошёл 2 пешеход
3)12+18=30 (км) – расстоянии е между пунктами
Ответ: 12 км; 18 км; 30 км.
Задачи на движение
Решение задач на движение
Решение задач на движение двух тел в противоположных направлениях.
Задача 1. Одновременно из одного пункта в противоположных направлениях вышли два пешехода. Один из них шёл со скоростью 6 км/ч, а другой 4 км/ч. Какое расстояние будет между ними через 3 часа?
? км
4 км/ч 6 км/ч
3 ч 3 ч
Решение
Скорость
|
Время
|
Расстояние
| |
1 пешеход
|
6 км/ч
|
3 ч.
|
? ?
|
2 пешеход
|
4 км/ч
|
3 ч.
|
?
|
1 способ: (6+4)*3=30 (км)
2 способ: 6*3+4*3=30 (км)
Ответ: 30 км.
Подписаться на:
Сообщения (Atom)